Relation/Funktion

Jede Menge geordneter Paare [x;y], bei der zu jedem x genau ein y gehört, heißt Funktion. Bei einer Relation können zu einem x mehrere verschiedene y zugeordnet sein.

Im Buch ² auf der Seite 66 finden Sie die grafische Darstellung der beiden Begriffe mittels Pfeildiagramm.

Beispiele

Eigenschaften von Funktionen

Schranken:

Eine Funktion heißt in einem Intervall nach unten beschränkt, wenn es eine Konstante K_u gibt, so dass für jedes x im betrachteten Intervall f(x) ≥ K_u gilt.

Die größte untere Schranke wird untere Grenze oder Infimum genannt.

Eine Funktion heißt in einem Intervall nach oben beschränkt, wenn es eine Konstante K_o gibt, so dass für jedes x im betrachteten Intervall f(x) ≤ K_o gilt.

Die kleinste obere Schranke wird obere Grenze oder Supremum genannt.

Beispiele

Monotonie:

Eine Funktion heißt in einem bestimmten Intervall monoton steigend, wenn für jedes beliebige x₂ > x₁ in diesem Intervall gilt: f(x₂) ≥ x₁.
Sie ist streng monoton steigend, wenn f(x₂) > x₁ gilt.

Eine Funktion heißt in einem bestimmten Intervall monoton fallend, wenn für jedes beliebige x₂ > x₁ in diesem Intervall gilt: f(x₂) ≤ x₁.
Sie ist streng monoton fallend, wenn f(x₂) < x₁ gilt.

Eine ausführliche Darstellung mit Beispielen finden Sie im Buch ² ab Seite 158.

Beispiele

Nullstelle:

Ein Argument x = x₀ einer Funktion f(x) heißt Nullstelle dieser Funktion genau dann, wenn gilt: f(x₀) = 0.

Nullstellen können mehrfach auftreten. Ist die Anzahl gerade, so wechselt der Graph an der Nullstelle nicht das Vorzeichen der Funktionswerte.

Im Buch ² wird ab Seite 181 das Thema "Nullstellen ganzrationaler Funktionen" behandelt.

Beispiele

Symmetrie:

Eine Funktion f(x) heißt gerade, wenn für alle x ∈ D gilt: f(−x) = f(x). Die Symmetrieachse ist die y-Achse.

Eine Funktion f(x) heißt ungerade, wenn für alle x ∈ D gilt: f(−x) = −f(x) bzw. f(x) = −f(−x). Es besteht Symmetrie zum Koordinatenursprung.

Außerdem ist es möglich, dass Funktionen andere Symmetrieachsen besitzen. Mittels einer Koordinatentransformation wird die Funktionsgleichung so verändert, dass die hier beschriebenen Symmetrieregeln gelten.

Im Buch ² wird ab Seite 154 das Thema Symmetrie behandelt.

Beispiele

Polstelle:

Polstellen sind eine Eigenschaft von Funktionen, bei denen Brüche auftreten. Hat die Nennerfunktion einer gebrochenen Funktion eine Nullstelle, die nicht zugleich Nullstelle der Zählerfunktion ist, so bezeichnet man dies als Polstelle (Unendlichkeitsstelle). Die Polstelle wird im Koordinatensystem mit einer Parallelen zur y-Achse durch den Punkt x_P dargestellt. Sie heißt Asymptote.

Beispiel

Lücke:

Ist die Polstelle der Nennerfunktion zugleich Nullstelle der Zählerfunktion, so handelt es sich um eine Lücke. Fällt die Lücke beim Umformen der Funktionsgleichung weg, so handelt es sich um eine hebbare Lücke.

Beispiel

Lineare Funktionen

Die linearen Funktionen sind ein Sonderfall der allgemeinen Polynomfunktion. Sie wurden bereits vor der Klassenstufe 11 behandelt. Schauen Sie unter Basiswissen nach, wenn Sie die grundlegenden Fakten wiederholen wollen.

Die Funktionsgleichung der Form f(x) = y = m·x + t wird explizite Form genannt.

Die Funktionsgleichung der Form a·x + b·y + c = 0 wird implizite Form genannt. Dabei gilt b≠0.

Für den Anstieg m gilt:

Der Bruch Δy/Δx heißt Differenzenquotient. Der Winkel α ist der Neigungswinkel der Geraden. Er liegt zwischen der positiven x-Achse und der Geraden. Er ist gegen den Uhrzeigersinn orientiert.

Eine Erläuterung der Winkelfunktionen im rechtwinkligen Dreieck befindet sich im Basiswissen.

Sind zwei auf einer Geraden liegenden Punkte bekannt, so lässt sich daraus die Funktionsgleichung f(x) ermitteln.

Zwei Geraden mit den Funktionsgleichungen h(x) = m₁·x + t und g(x) = m₂·x + n stehen im Schnittpunkt senkrecht zueinander, wenn m₁·m₂ = −1 gilt.

Beispiele

Quadratische Funktionen und Gleichungen

Die quadratischen Funktionen sind ein Sonderfall der allgemeinen Polynomfunktion. Sie wurden bereits vor der Klassenstufe 11 behandelt. Schauen Sie unter Basiswissen nach, wenn Sie die grundlegenden Fakten wiederholen wollen.

Potenzfunktionen

Die Funktion f(x) = xⁿ mit x∈R und n∈Z^* heißt Potenzfunktion vom Grad n.

Für n = −2, ..., +3 sollten Sie die Funktionsgraphen aus früheren Schuljahren kennen.

Beispiele

Polynomfunktion

Die Funktion f(x) = a_n·xⁿ +  a_n−1·xⁿ⁻¹ + a_n−2·xⁿ⁻²  + ... + a₁·x¹ + a₀ mit x∈R, n∈N, a∈R und a_n≠0 heißt ganzrationale Funktion (Polynomfunktion) vom Grad n.

Eine weitere Schreibweise ist 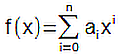. (Σ ist das Zeichen für "Summe".)

Exponentialfunktion

Die Funktion f(x) = a^x mit a, x∈R und a>0, a≠1 heißt Exponentialfunktion.

Von besonderer Bedeutung ist der Fall a = e: f(x) = e^x
Je nach Funktionsgleichung unterscheidet man drei typische Kurvenverläufe: Wachstum, Zerfall und Sättigung.

Die Zahl e ist der Grenzwert der unendlichen Zahlenfolge 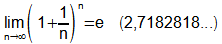mit n∈N und wird "Eulersche Zahl" genannt.

Beispiel Wachstumsvorgang   Beispiel Zerfallsvorgang   Beispiel Sättigungsvorgang   Beispiele a^x

Periodische Funktionen

*** wird noch erstellt ***

Umkehrfunktion

*** wird noch erstellt ***

Regression

*** wird noch erstellt ***

Einfluss von Parametern

*** wird noch erstellt ***