Begriffe:

Die Trigonometrie ist ein Teilgebiet der Mathematik, welches sich mit Berechnungen am Dreieck mit Hilfe der Winkelfunktionen beschäftigt.

Zur Definition der Winkelfunktionen verwendet man beim rechtwinkligen Dreieck die Begriffe Ankathete (am Winkel anliegend) und Gegenkathete (dem Winkel gegenüberliegend).

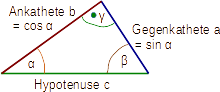
Sinus:

Der Sinus eines Winkels ist definiert als das Verhältnis von Gegenkathete/Hypotenuse . Für den Winkel α gilt dann sin α = a/c.

Da die Hypotenuse c die längste Seite im rechtwinkligen Dreieck ist, ist der Qotient der beiden Seitenlängen immer kleiner als 1.

Nimmt man für die Länge der Hypotenuse c den Wert 1 an, dann wäre der Wert sin α die Länge der Gegenkathete a.
Hat die Hypotenuse c eine beliebige Länge, dann ist sin α ein Faktor, um den die Gegenkathete a kürzer ist als die Hypotenuse c.

Eine Beschreibung der Sinusfunktion und ihrer Eigenschaften finden Sie im Basiswissen unter "Funktionale Zusammenhänge".

Cosinus (Kosinus):

Der Cosinus eines Winkels ist definiert als das Verhältnis von Ankathete/Hypotenuse . Für den Winkel α gilt dann cos α = b/c.

Da die Hypotenuse c die längste Seite im rechtwinkligen Dreieck ist, ist der Qotient der beiden Seitenlängen immer kleiner als 1.

Nimmt man für die Länge der Hypotenuse c den Wert 1 an, dann wäre der Wert cos α die Länge der Ankathete b.
Hat die Hypotenuse c eine beliebige Länge, dann ist cos α ein Faktor, um den die Ankathete b kürzer ist als die Hypotenuse c.

Tangens:

Der Tangens eines Winkels ist definiert als das Verhältnis von Gegenkathete/Ankathete . Für den Winkel α gilt dann tan α = a/b.

Der Tangens eines Winkels entspricht dem Anstieg m einer linearen Funktion (siehe Kursstufe 11).