Lineare Funktion

Gegeben sind die Funktionen f(x), g(x), h(x) und k(x) mit ihren Funktionsgraphen.

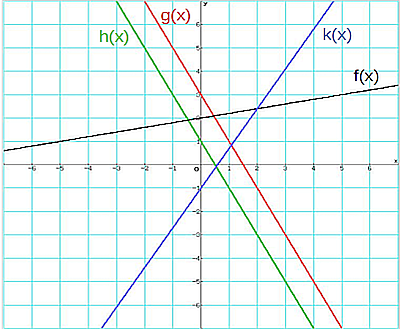
Beispiel 1:

Der Anstieg m der Geraden g(x) lässt sich aus dem Differenzenquotienten ermitteln, indem man ein geeignetes Anstiegsdreieck verwendet. Der Funktionsgraph ist monoton fallend. Der Anstieg m ist negativ.
m = −2/1 = −2

Der Parameter t, d. h. der y-Achsenabschnitt, ist aus dem Koordinatensystem ablesbar: t = 3

Funktionsgleichung in expliziter Form: g(x) = y = −2·x + 3

Funktionsgleichung in impliziter Form: 0 = 2·x + y − 3

Beispiel 2:

Die Gerade h(x) liegt parallel zur Geraden g(x). Ihre Anstiege sind gleich.
m = −2

Der Parameter t, d. h. der y-Achsenabschnitt, ist aus dem Koordinatensystem ablesbar: t = 1

Funktionsgleichung in expliziter Form: h(x) = y = −2·x + 1

Funktionsgleichung in impliziter Form: 0 = 2·x + y − 1

Beispiel 3:

Die Gerade f(x) geht durch die Punkte P₁(0;2) und P₂(5;3). Der Anstieg m wird mittels dem Differenzenquotienten berechnet.
m = (3 −2)/(5 −0) = 1/5 = 0,2

Der Parameter t, d. h. der y-Achsenabschnitt, ist aus dem Koordinatensystem ablesbar: t = 2

Funktionsgleichung in expliziter Form: f(x) = y = 0,2·x + 2

Funktionsgleichung in impliziter Form: 0 = −0,2·x +  y − 2

Beispiel 4:

Die Gerade k(x) geht durch die Punkte P₁(0;−1) und P₂(3;4). Der Anstieg m wird mittels dem Differenzenquotienten berechnet.
m = (4 −(−1))/(3 −0) = 5/3

Der Parameter t, d. h. der y-Achsenabschnitt, ist aus dem Koordinatensystem ablesbar: t = −1

Funktionsgleichung in expliziter Form: f(x) = y = 5/3·x − 1

Funktionsgleichung in impliziter Form: 0 = −5/3·x +  y + 1

Beispiel 5:

Gesucht ist die Gleichung einer Geraden, welche durch den Punkt P(2;−3) und senkrecht zur Geraden h(x) verläuft.

Für den Anstieg gilt m·(−2) = −1 und damit m = 1/2.

Die Gleichung im Punkt P lautet: −3 = 1/2·2 + t
t = −3 − 1 = −4

Funktionsgleichung in expliziter Form: f(x) = y = 1/2·x − 4

Funktionsgleichung in impliziter Form: 0 = −1/2·x +  y + 4

Beispiel 6:

Gesucht sind die Koordinaten des Schnittpunktes der Geraden h(x) und k(x).

Durch Gleichsetzen der beiden Funktionsgleichungen erhält man: −2·x + 1 = 5/3·x - 1.

Die Gleichung wird umgeformt und zusammengefasst: 1 + 1 = 5/3·x + 2·x bzw. 2 = 11/3·x

Die Gleichung wird nach x aufgelöst: x = 6/11

Das Ergebnis wird in eine Funktionsgleichung (z. B. h(x)) eingesetzt und der Funktionswert y berechnet.
h(6/11) = −2·6/11 + 1 = −1/11

Die Geraden h(x) und k(x) schneiden sich im Punkt S(6/11;−1/11).

Beispiel schließen