Monotonie

Die Funktion f(x) = x² + 1 ist für alle {x| x∈R und x < 0} streng monoton fallend.
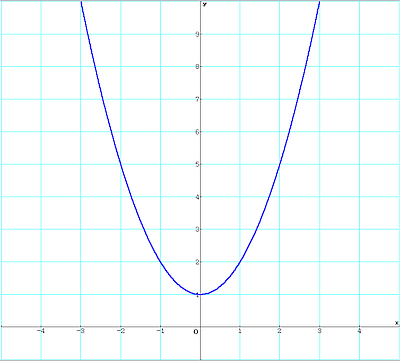
Für alle {x| x∈R und x > 0} ist sie streng monoton steigend.

Die Funktion f(x) = 4·x + 5 ist für alle x∈R streng monoton steigend.

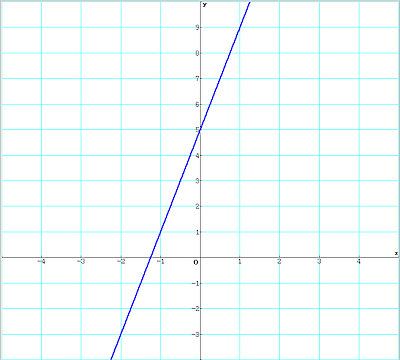
Der rechnerische Nachweis beruht darauf, dass man z. B. bei einer monoton wachsenden Funktion mit x₁ < x₂ und x₁ − x₂ < 0 den Nachweis führt, dass auch f(x₁) − f(x₂) < 0 gilt.

Rechnerischer Nachweis der Monotonie für das Beispiel f(x) = 4·x + 5 mit x∈R:

Festlegung: x₁ < x₂ und x₁, x₂ ∈ R
Dann gilt: f(x₁) − f(x₂) = (4·x₁ + 5)  − (4·x₂ + 5) = 4·x₁ −  4·x₂ = 4·(x₁ − x₂)
Der Ausdruck x₁ − x₂ ist kleiner als 0, d. h. f(x₁)  − f(x₂) ist ebenfalls kleiner als 0. Damit ist die Funktion f(x) streng monoton wachsend.

Rechnerischer Nachweis der Monotonie für das Beispiel f(x) = x²+1 mit x∈R:

Festlegung: x₁ < x₂ und x₁, x₂ ∈ R
Dann gilt: f(x₁) − f(x₂) = (x₁² + 1)  − (x₂² + 1) = x₁² −  x₂² = (x₁ − x₂)· (x₁ + x₂)
Der Ausdruck x₁ − x₂ ist aufgrund der Festlegung kleiner als 0.
Der Ausdruck (x₁ + x₂) muss größer als Null sein, wenn das Produkt kleiner als Null sein soll. Für die Summe zweier Zahlen gilt dies nur, wenn beide Zahlen größer als Null sind. Sind beide Zahlen negativ, so würde die Summe auch ein negatives Vorzeichen besitzen und das Produkt insgesamt dann größer als Null sein.
Dies zeigt, dass es bei x = 0 einen Wechsel der Monotonie gibt. Monoton wachsend ist die Funktion nur bei x∈R₊.

Beispiele schließen