Begriffe:
Term:
Ein Term ist ein mathematischer Ausdruck zur Berechnung eines Wertes.
Er kann aus Zahlen, Klammern, Rechenzeichen und Variablen bestehen. Beispiel: 5 · x + 2
Variable:
Variablen sind Platzhalter für beliebige Zahlen. Für sie
werden Kleinbuchstaben verwendet.
Termwert:
Für die Berechnung des Termwertes müssen Variablen durch
Zahlen ersetzt werden.
Variablengrundbereich:
Darunter versteht man die Zahlenmenge, aus der man
für eine Variable konkrete Zahlenwerte zur Termwertberechnung auswählen kann.
Beispiel:
5 · x + 2 (x ∈N), d. h. es dürfen für x die Zahlen 0, 1, 2, 3, ...
eingesetzt werden.
Bei Funktionen nennt man den Variablengrundbereich für x Definitionsbereich und die Menge der daraus resultierenden Funktionswerte y Wertebereich.
Lösungsmenge:
Damit bezeichnet man die Menge aller Werte einer Variablen,
für die beim Einsetzen eine wahre Aussage bei Gleichungen oder Ungleichungen entsteht. Beispiel:
5 · x + 2 = 12 (x ∈N); L = {2}
Lineare Gleichungen:
Die Variablen in einer Gleichung sind nur mit dem Exponenten 1 vorhanden.
Beispiel:
-x + 2 = 2 · x - 7 (x ∈N)
Durch Umstellen erhält man: 2 + 7 = 2 · x + x und durch Zusammenfassen entsteht dann 9 = 3 · x. Da x = 3 ein Element des Variablengrundbereichs ist, besitzt die Gleichung eine Lösung. L = {3}
Die Lösung der Gleichung lässt sich auch grafisch ermitteln. Dazu stellt man beide Seiten der Gleichung als lineare Funktion im Koordinatensystem dar. Schneiden sich die Funktionsgraphen, so gibt es eine mögliche Lösung. Abschließend muss geprüft werden, ob die ermittelte Lösung zum Variablengrundbereich gehört.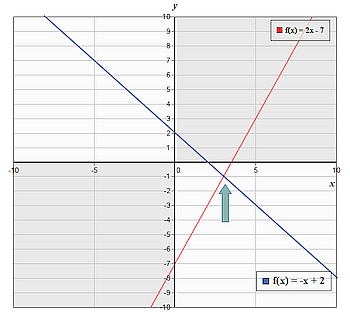
Lineare Funktionen:
Die Funktion y = f(x) enthält nur x¹. Legt man als Variablengrundbereich die Menge R der reellen Zahlen fest, so entsteht bei der Darstellung im Koordinatensystem eine Gerade. Um den Funktionsgraphen zeichnen zu können, genügt es, für zwei verschiedene x (Argumente) den Funktionswert zu berechnen.
Allgemeine Form der Funktionsgleichung: y = m · x + n (m: Anstieg, Steigung; n: y-Achsenabschnitt)
Beispiel:
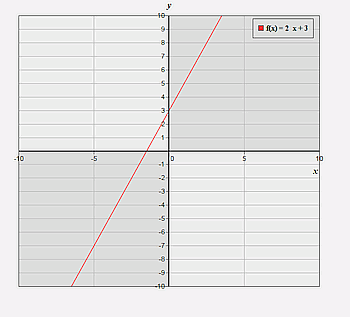
y = 2 · x + 3 (x ∈R)
Definitions- und Wertebereich sind die reellen Zahlen. Der Anstieg m ist 2. Der Wert von n ist der Funktionswert für x = 0: y = f(0) = 3.
Die Nullstelle der Funktion erhält man, wenn man die lineare Gleichung 0 = 2 · x + 3 löst. Die Lösung ist x = -3/2 = -0,5.
Die lineare Funktionen werden in Klassenstufe 11 fortgesetzt.