Begriffe:
Term:
Ein Term ist ein mathematischer Ausdruck zur Berechnung eines Wertes.
Er kann aus Zahlen, Klammern, Rechenzeichen und Variablen bestehen. Beispiel: 5 · x + 2
Variable:
Variablen sind Platzhalter für beliebige Zahlen. Für sie
werden Kleinbuchstaben verwendet.
Termwert:
Für die Berechnung des Termwertes müssen Variablen durch
Zahlen ersetzt werden.
Variablengrundbereich:
Darunter versteht man die Zahlenmenge, aus der man
für eine Variable konkrete Zahlenwerte zur Termwertberechnung auswählen kann.
Beispiel:
5 · x + 2 (x ∈N), d. h. es dürfen für x die Zahlen 0, 1, 2, 3, ...
eingesetzt werden.
Bei Funktionen nennt man den Variablengrundbereich für x Definitionsbereich und die Menge der daraus resultierenden Funktionswerte y Wertebereich.
Lösungsmenge:
Damit bezeichnet man die Menge aller Werte einer Variablen,
für die beim Einsetzen eine wahre Aussage bei Gleichungen oder Ungleichungen entsteht. Beispiel:
5 · x + 2 = 12 (x ∈N); L = {2}
Quadratische Funktionen:
Quadratische Funktionen enthalten als höchste Potenz x². Der Funktionsgraph ist die Parabel. Der Scheitelpunt ist entweder ein minimaler oder ein maximaler Funktionswert. Der Definitionsbereich und der Wertebereich sind die Menge der reellen Zahlen.
Die einfachste Funktionsgleichung ist f(x) = a · x2 + c mit a, c, x ∈R, a≠0.
Allgemeine Form der Funktionsgleichung: f(x) = y = a · x 2 + b · x + c mit a, b, c, x ∈R, a≠0
Als Normalform der quadratischen Funktionsgleichung bezeichnet man die Form f(x) = y = x2 + p · x + q mit p, q, x ∈R
Beispiel 1:
Die Funktionsgleichung f(x) = 3·x² + 6·x −9 lässt sich umformen in: f(x) = 3·(x² + 2·x −3) mit p = b/a = 6/3 = 2 und q = c/a = −9/3 = −3
Eine weitere Form der Funktionsgleichung ist die Scheitelpunktsform der Funktionsgleichung. Sie entsteht durch Umformen mittels der quadratischen Ergänzung aus der Normalform.
Beispiel 2:
Gegeben ist die Funktionsgleichung f(x) = 3·(x² + 2·x −3) aus
Beispiel 1. Der Wert von p (hier: 2) wird halbiert und anschließend quadriert: p/2 =
2/2 = 1 → 1² = 1. Die quadratische Ergänzung ist damit 1.
Die Funktionsgleichung lautet nun: f(x) = 3·(x² + 2·x +
1 −1 −3) = 3·((x+1)² − 1 − 3) =
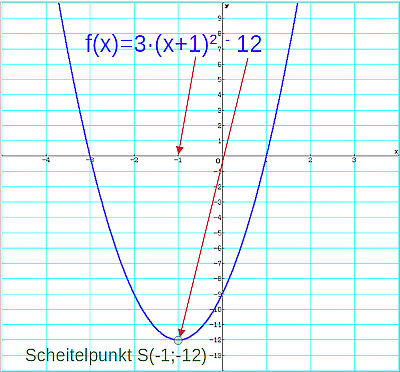
3·((x+1)² − 4) = 3·(x+1)² − 12
.
Quadratische Gleichungen:
In einer Gleichung sind Variablen mit dem Exponenten 2 vorhanden. Ihre allgemeine Form lautet: a · x² + b · x + c = 0 mit a, b, c, x ∈R, a≠0
Das Lösen einer quadratischen Gleichung verwendet man zum Bestimmen der Nullstellen einer quadratischen Funktion. Für die Lösung wird das Radizieren ("Wurzelziehen") benötigt. Dabei ist zu beachten, dass diese Rechenoperation im Bereich der reellen Zahlen nur für einen positiven RadikandenDer Radikand ist der Ausdruck unter dem Wurzelzeichen. definiert ist. Weiterhin ist zu beachten, dass die Quadratwurzel zwei Lösungen besitzt (√4 = −2 bzw. √4 = +2).
Beispiel 1:
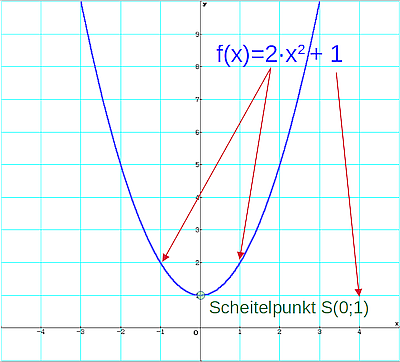
Gegeben ist die Gleichung 0 = 2·x²+1. Durch Umformen ergibt sich −1/2 = x². Im Variablengrundbereich x∈R gibt es keine Lösung der Gleichung. Die Funktionsgleichung f(x) = 2·x²+1 besitzt keine Nullstellen (siehe Abbildung).
Beispiel 2:
Gegeben ist die Gleichung 0 = 3·x² + 6·x −9. Ist die
Scheitelpunktsform bekannt, so lässt sich die Gleichung durch Umformen lösen:
3·(x+1)² − 12 = 0
(x+1)² = 12/3
x+1 = √(4)
x = −1 + √(4)
Damit ergeben sich die Lösungen x1 = −1 −2 = −3 und x2 = −1 +2 = 1. Die Funktion f(x) = 3·x² + 6·x −9 besitzt zwei Nullstellen (siehe Abbildung).
Eine weitere Möglichkeit ist die Verwendung der allgemeinen Lösungsformel:
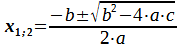
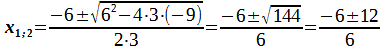
Die quadratischen Funktionen werden in Klassenstufe 11 fortgesetzt.