Symmetrie

Für die Funktion f(x) = x² gilt: f(−x) = (−x)²  = x² = f(x)
Die Funktion ist symmetrisch zur y-Achse.

Für die Funktion f(x) = x³ gilt: f(−x) = (−x)³  = −x³ = −f(x)
Die Funktion ist symmetrisch zum Koordinatenursprung.

Für die Funktion f(x) = 2·x² − 4·x gilt:
f(−x) = 2·(−x)² − 4·(−x) = 2·x² + 4·x 
−f(x) = −(2·x² − 4·x) = −2·x² + 4·x
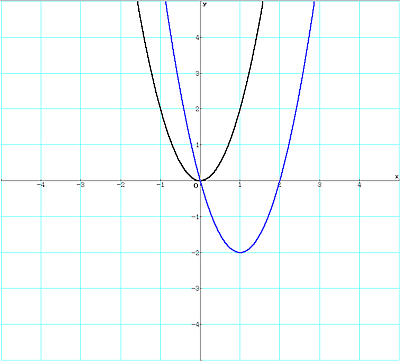
Die Funktion ist weder symmetrisch zum Koordinatenursprung bzw. zur y-Achse.
Allerdings ist sie symmetrisch zu einer Parallelen der y-Achse durch den Punkt x = 1.

Lineare Koordinatentransformation

Mit der Koordinatentransformation wird ein neues Koordinatensystem so positioniert, dass bei einer gegebenen Funktionsgleichung die Achsen- oder Punktsymmetrie abgelesen werden kann. Nachfolgend wird die Vorgehensweise für f(x) = 2·x² − 4·x beschrieben.

1. Gleichung umformen: y = 2·(x² − 2·x) (Normalform der quadratischen Funktion herstellen)
2. Binomische Formel anwenden und quadratisch ergänzen: y = 2·((x −1)² − 1) (Weil (x −1)² = x² − 2·x + 1 ergibt, muss 1 subtrahiert werden.)
3. Ausmultiplizieren: y = 2·(x −1)² − 2 (Wir haben die Scheitelgleichung der quadratischen Gleichung hergestellt.)

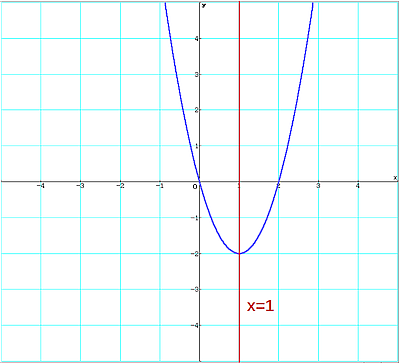
Aus der letzten Gleichung wird ersichtlich, dass sich der Scheitelpunkt der Parabel im Punkt S(1,-2) befindet. Die Symmetrieachse ist die Parallele zur y-Achse mit x=1.

Jetzt beginnt die eigentliche Koordinatentransformation.

1. Umstellen: y + 2 = 2·(x −1)²
2. Koordinaten ersetzen: x_neu = x - 1 sowie y_neu = y + 2
3. Neue Funktionsgleichung notieren: f(x_neu) = 2·x_neu²

Alle Koordinaten des alten Koordinatensystems wurden mit x − 1 und y + 2 verschoben.

Für die neue Funktionsgleichung lässt sich die Achsensymmetrie nachweisen: f(−x_neu) = (−x_neu)² = 2·x_neu² = f(x_neu)

Beispiele schließen