Exponentialfunktion

Wachstumsvorgang:

Die allgemeine Funktionsgleichung lautet: f(x) = a·e^k·x mit a, k, x ∈ R, a>0, k>0

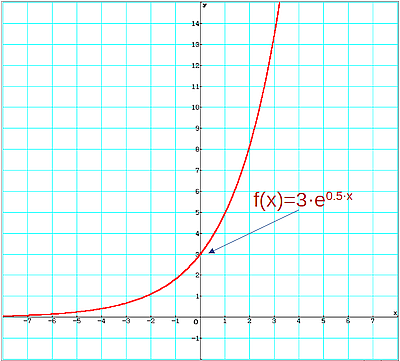
Anwendungsbeispiel:

Bei einem biologischen Experiment werden 1000 Bakterien in eine Nährlösung gebracht. Ihre Anzahl verdreifacht sich stündlich. Gesucht ist eine Funktionsgleichung für das Bakterienwachstum.

Mit dem Startwert von 1000 Bakterien zum Zeitpunkt 0 lässt sich der Faktor a bestimmen:
1000 = a·e^k·0 = a·e⁰ = a·1 = a

Mit einem weiteren Zahlenpaar aus der Tabelle wird jetzt der Wert für k ermittelt:
8000 = 1000·e^k·3   Nach der Division durch 1000 entsteht: 8 = e^k·3

Zur Lösung gibt es zwei Möglichkeiten:

1. Die letzte Gleichung muss nun nach x aufgelöst werden. Hierfür benötigt man den Logarithmus: k·3 = log_e(8), d. h. k = 1/3·log_e(8) = 1/3·ln (8)
2. Man nutzt einen Taschenrechner mit CAS: solve(8=e^k·3,k)

Das Ergebnis k ≈ 0,69315 liefert folgende Funktionsgleichung für das Bakterienwachstum: f(x) = 1000·e^0,69315·x

Nach den Potenzgesetzen gilt auch: f(x) = 1000·(e^0,69315)^x  = 1000·2^x

Die Funktionsgleichung bezieht sich darauf, dass der für die Variable x eingesetzte Zahlenwert mit der Einheit "Stunde" verwendet wird.

Beispiele schließen