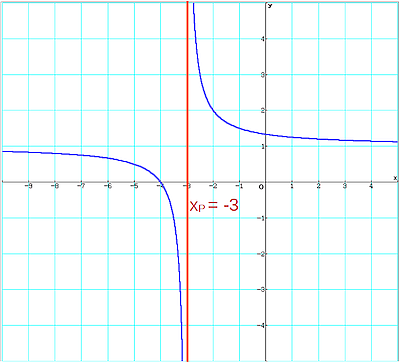
Polstelle
Gegeben ist die Funktion f(x) = (4 + x)/(x + 3).
Der Nenner x + 3 darf nicht den Wert 0 annehmen. Für x = −3 ist die Division
nicht erlaubt.
Der Zähler hat bei x = −3 den Wert 1.
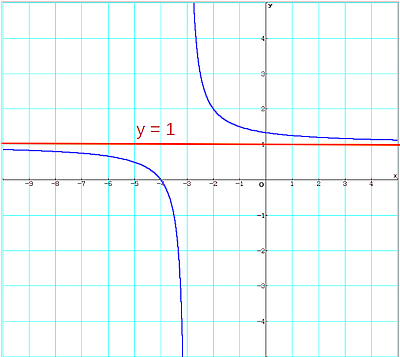
Die Funktion f(x) = (4 + x)/(x + 3) besitzt bei x = −3 eine Polstelle. Ihr Definitionsbereich ist daher { x | x∈R und x≠−3 }
Ergänzung:
Der Funktionsgraph lässt vermuten, dass es bei y = 1 eine weitere Asymptote gibt. Ihre Funktionsgleichung erhält man, wenn man die Gleichung von f(x) etwas umformt. (Diese Asymptote hat nichts mit der Polstelle zu tun.)
Der Zähler lässt sich schreiben als (x + 3) + 1. Eine gültige Umformung der Funktionsgleichung ergibt sich, wenn man die beiden Summanden des Zählers jeweils durch den Nenner (x + 3) dividiert: f(x) = (x + 3)/(x + 3) + 1/(x + 3) = 1 + 1/(x + 3).
Zu diesem Ergebnis kommt man auch, wenn man mit dem Taschenrechner die Funktion propFrac(...) ausführt.
Der Dezimalwert des Bruches 1/(x + 3) wird bei wachsendem (+∞) bzw. kleiner werdenden x (−∞) immer kleiner, d. h. er strebt gegen Null. Zu 1 wird eine kleiner werdende Zahl addiert bzw. von 1 abgezogen.