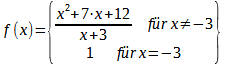Lücke
Gegeben ist die Funktion f(x) = (x2 + 7·x + 12) /(x + 3).
Der Nenner x + 3 darf nicht den Wert 0 annehmen. Für x = −3 ist die Division
nicht erlaubt.
Setzt man x = −3 im Zähler ein, so ergibt sich hier ebenfalls der
Wert Null.
Die Funktion f(x) = (x2 + 7·x + 12)/(x + 3) besitzt bei x = −3 eine Lücke. Ihr Definitionsbereich ist daher { x | x∈R und x≠−3 }
Der Zähler (x2 + 7·x + 12) lässt sich z. B. mittels Polynomdivision zerlegen in (x + 3)·(x + 4). Der Faktor (x + 3) wird gekürzt und die Lücke ist damit "behoben". Es ergibt sich die Funktionsgleichung f(x) = x + 4. Der Definitionsbereich ist x∈R.
Bezogen auf die ursprüngliche Funktionsgleichung muss man schreiben: