Begriffe:

Variablengrundbereich:
Darunter versteht man die Zahlenmenge, aus der man für eine Variable konkrete Zahlenwerte zur Termwertberechnung auswählen kann.
Beispiel: 5 · x + 2 (x ∈N), d. h. es dürfen für x die Zahlen 0, 1, 2, 3, ... eingesetzt werden.

Bei Funktionen nennt man den Variablengrundbereich für x Definitionsbereich und die Menge der daraus resultierenden Funktionswerte y Wertebereich.

Lösungsmenge:
Damit bezeichnet man die Menge aller Werte einer Variablen, für die beim Einsetzen eine wahre Aussage bei Gleichungen oder Ungleichungen entsteht. Beispiel: 5 · x + 2 = 12 (x ∈N); L = {2}

Winkel und Einheiten:
Die Größe eines Winkels kann im Gradmaß oder im Bogenmaß angegeben werden. Beim Gradmaß wird der Drehung im Vollkreis das Maß 360 mit der Einheit Grad (°) zugeordnet. Beim Bogenmaß wird dem Winkel das Verhältnis von Kreisbogenlänge/Radius zugeordnet. Die Einheit ist rad (Radiant). Beim Verwenden des Taschenrechners muss auf die richtige Einstellung von Gradmaß oder Bogenmaß geachtet werden.

Beim einem Radius r = 1 entspricht die Bogenlänge b dem Bogenmaß des Winkels α.
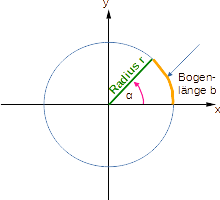
Der Umfang des Vollkreises (Winkel 360°) entspricht dann 2·π rad bzw. es gilt 180° = π rad.

Potenzfunktionen:

Im Mathematikunterricht bis Klassenstufe 10 wurde die Potenzfunktion mit y = a·xⁿ und a, x∈R; n∈{-2, -1, 1, 2, 3} behandelt.

Da die Potenzfunktionen in der Klassenstufe 11 in gleicher Weise verwendet werden, finden Sie die Eigenschaften und Funktionsgraphen im Lernbereich 3 der Klassenstufe 11.

Exponentialfunktion:

Aus dem Mathematikunterricht bis Klassenstufe 10 sollte die Exponentialfunktion mit y = c·a^x bekannt sein.

Da die Exponentialfunktionen in der Klassenstufe 11 behandelt werden, finden Sie die Eigenschaften und Funktionsgraphen im Lernbereich 3 der Klassenstufe 11.

Sinus-Funktion:

Die Definition der Winkelfunktion sin α können Sie unter Winkelfunktionen im rechtwinkligen Dreieck nachlesen.

Die vier Abbildungen stellen das rechtwinklige Dreieck mit der Hypotenuse c = 1 und dem Winkel α in den einzelnen Quadranten des Koordinatensystems dar. Die Hypotenuse c ist gleichzeitig der Radius eines Kreises.

Die Werte von sin α sind größer als Null.
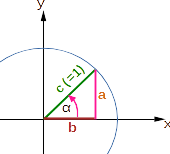
Der Winkel α liegt zwischen 0° und 90° bzw. zwischen 0 und π/2.

Die Werte von sin α sind größer als Null.
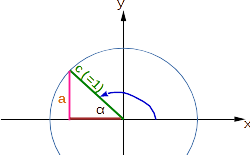
Der mathematische Winkel liegt zwischen 90° und 180° bzw. zwischen π/2 und π.
Der Winkel im Dreieck wird mit 180°−α angegeben.

Es gilt: sin(α) = sin(180°-α)

Die Werte von sin α sind kleiner als Null.
Der mathematische Winkel liegt zwischen 180° und 270° bzw. zwischen π und (3/2)·π.
Der Winkel im Dreieck wird mit α+180° angegeben.

Es gilt: −sin(α) = sin(180°+α)

Die Werte von sin α sind kleiner als Null.
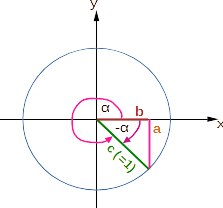
Der Winkel α liegt zwischen 270° und 360° bzw. zwischen (3/2)·π und 2·π.

Die obigen Darstellungen werden Zeigerdarstellung genannt. Dreht man die Hypotenuse c gegen den Uhrzeigersinn von 0° bis 360°, so lässt sich jedem Winkel ein Punkt auf dem Kreisbogen zuordnen.

Stellt man den Zusammenhang zwischen dem Winkel α und dem Wert sin α (= Länge der Seite a) in einem Koordinatensystem dar, so ergibt sich ein periodisch verlaufender Funktionsgraph. Zu beachten ist dabei, dass der Winkel auf der x-Achse im Bogenmaß angegeben wird.

Die Sinus-Funktion besitzt bei y = 1 ein Maximum und bei y = −1 ein Minimum. Der Funktionsgraph ist symmetrisch zum Koordinatenursprung.

Die Sinusfunktion hat eine Periode von 2π (360°). Der Winkel α = 380° entspricht dem Winkel α = 380°−360° = 20°. Damit gilt auch für den Funktionswert sin(380°)  = sin(20°). Ist ein Funktionswert gegeben, so lassen sich diesem verschiedene Winkel zuordnen. Dies ist in der Abbildung beispielhaft mit den grünen Punkten dargestellt.

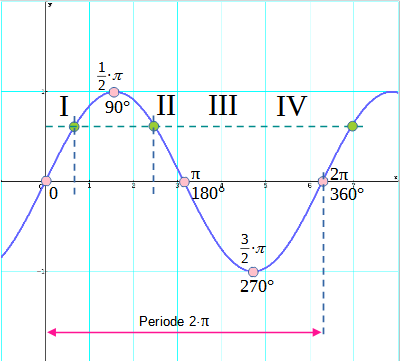
Die römischen Zahlzeichen beziehen sich auf den jeweiligen Quadranten im Koordinatensystem des Zeigerdiagramms.

Durch zusätzliche Parameter lässt sich der Funktionsgraph verändern.

Der Parameter a ändert nicht die Periode. Er verändert Maximum und Minimum.
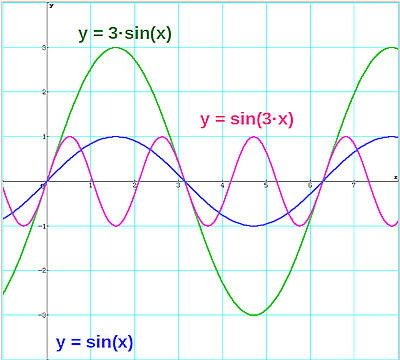
Der Parameter b verändert die Periode. Maximum und Minimum bleiben unverändert.

Die Sinusfunktion wird auch in der Klassenstufe 11 behandelt.