Inhalt:
Bei allen Aufgaben ist ein vollständiger Lösungsweg anzugeben.
Eigenschaften von Funktionen
Aufgabe 1: Eigenschaften einer Funktion bestimmen
Für die beiden Funktionen f(x) und g(x) sind die nachfolgend genannten Eigenschaften zu ermitteln. Zusätzlich ist das Schaubild der Funktion im Koordinatensystem darzustellen. Die Genauigkeit bei Berechnungen und Lösungen beträgt zwei Nachkommastellen. Die Lösungen sind zu erläutern.
Monotonie, Nullstellen, Symmetrie, Schranken, Polstellen, Lücken
Funktion 1:
f(x) = 1/4·x4 − 2·x2 −3
Funktion 2:
g(x) = (x2 + x -12) / (1/2·x2 + 3·x +4)
Lineare Funktionen
Aufgabe 2: Funktionsgleichung ermitteln
Ermitteln Sie die Geradengleichungen f(x), g(x) und h(x). Verwenden Sie die Form y = m · x + t.
Beispiel 1:
P1 (-3 ; -3) und m = 2,5
f(x) = ?
Beispiel 2:
P1 (1 ; -2) und P2 (-3 ; -14)
g(x) = ?
Beispiel 3:
P1 (3 ; -7) und P2 (-2 ; 5)
h(x) = ?
Aufgabe 3: Funktionsgleichung ermitteln
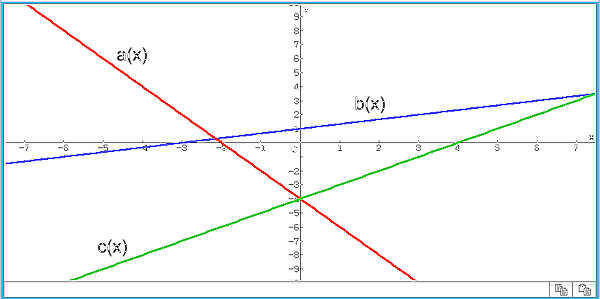
Die Abbildung zeigt ein Koordinatensystem mit den drei Funktionsgraphen a(x), b(x) und c(x).
Ermitteln Sie die Gleichungen in der Form y = m · x + t.
Aufgabe 4: Nullstelle ermitteln
Berechnen Sie die Nullstellen für die Funktionsgleichungen f(x), g(x) und h(x) aus Aufgabe 1.
Aufgabe 5: Schnittpunkte bestimmen
Berechnen Sie die Schnittpunkte für die Funktionen a(x) und b(x), a(x) und c(x) bzw. b(x) und c(x) aus Aufgabe 3.
Aufgabe 6: Geradengleichung ermitteln
Diese Aufgabe bezieht sich auf die Abbildung von Aufgabe 3. Die Gerade mit der Gleichung d(x) soll senkrecht zur Geraden b(x) und durch den Punkt P(0 ; 1) verlaufen. Wie lautet die Gleichung d(x)?
Aufgabe 7: Wertetabelle und Geradengleichung
Gegeben ist die Wertetabelle einer linearen Funktion. Ermitteln Sie die Funktionsgleichung und geben Sie diese in der impliziten Form an.
| x | -1 | 0 | 1 | 2 |
| y | 6 | 5,3 | 4,6 | 3,9 |
Zugelassene Hilfsmittel
Formelsammlung, Taschenrechner