In einer Urne befinden sich eine rote, eine blaue und eine gelbe Kugel. Im Zufallsexperiment werden zwei Kugeln ohne zurücklegen entnommen. Die Reihenfolge der entnommenen Kugeln ist nicht von Interesse.

• Berechnen Sie die Anzahl der Möglichkeiten für die entnommenen Kugeln.
• Geben Sie den Ergebnisraum Ω an.
• Ereignis E1: "Unter den entnommenen Kugeln befindet sich eine rote Kugel."
  Notieren Sie das Ereignis E1 in Mengenschreibweise.
• Formulieren Sie für das Experiment ein unmögliches Ereignis E2.
• Formulieren Sie ein sicheres Ereignis E3.

Der Farbton eines Behälters wird während der Herstellung durch das Mischen von vier verschiedenen Farben erreicht. Bei der Endkontrolle wurde festgestellt, dass das Ereignis E1 eintritt. Die entsprechenden Häufigkeiten sind in der Tabelle dargestellt.

E1 = "Der Behälter hat nicht den gewünschten Farbton."

produzierte Anzahl	50	100	500	2000	5000	10000	20000
E1 ist eingetreten	2	5	21	83	210	422	839

Ermitteln Sie die relativen Häufigkeiten. Lässt sich aus diesen Daten eine Wahrscheinlichkeit abschätzen, mit der das Ereignis E1 eintritt und was bedeutet dies für eine produzierte Stückzahl von 50000 Behältern?

In der Urne U1 befinden sich zwei gelbe und zwei rote Kugeln. In der Urne U2 befinden sich eine gelbe und eine rote Kugel. Aus der Urne U1 wird eine Kugel gezogen, die Farbe notiert und in die Urne U2 gelegt. Anschließend wird aus der Urne U2 eine Kugel gezogen und die Farbe notiert.

a) Geben Sie den Ergebnisraum Ω an.
b) Erstellen Sie für das beschriebene Zufallsexperiment ein Baumdiagramm mit Angabe der Wahrscheinlichkeiten.
c) Berechnen Sie die Wahrscheinlichkeiten für alle Elementarereignisse.

Ereignis A = "Die notierte Farben sind 'Rot-Gelb'."
Ereignis B = "Die erste notierte Farbe ist 'Rot'."
Ereignis C = "Es wurden zwei gleiche Farben notiert."

d) Notieren Sie die Mengenschreibweise für die Ereignisse A, B und C.
e) Bestimmen Sie für jedes Ereignis die Wahrscheinlichkeit seines Eintretens.
f) Prüfen Sie, ob die Ereignisse A und B bzw. die Ereignisse B und C voneinander stochastisch abhängig sind.

Von 2000 befragten Haushalten gaben 23% an, keine Bücher zu lesen. 1100 Haushalte besuchen kein Fitness-Studio. Von den Haushalten, welche keine Bücher lesen, gaben 30% an, regelmäßig ins Fitness-Studio zu gehen. Ein Haushalt wird zufällig auswählt.

Mit welcher Wahrscheinlichkeit werden in einem Haushalt sowohl Bücher gelesen und auch ein Fitness-Studio besucht?
Mit welcher Wahrscheinlichkeit werden in einem Haushalt keine Bücher gelesen, wenn bereits bekannt ist, dass ein Fitness-Studio besucht wird?

Lösen Sie diese Aufgabe mit einer Vierfeldertafel.

In einer XY-Ebene liegen 7 verschiedene Punkte (P1, P2, ..., P7). Es liegen niemals mehr als zwei Punkte auf ein und derselben Geraden. Welche Wahrscheinlichkeit hat das Ereignis "P1 und P7 liegen auf der Geraden", wenn zwei Punkte zufällig ausgewählt werden?

Beschreiben Sie ein passendes Urnenmodell und ermitteln Sie die Lösung.

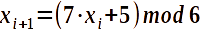
Welche Zufallszahlenfolge generiert diese Formel, wenn man mit x=4 beginnt?