Die Stochastik besteht aus den Gebieten Statistik und Wahrscheinlichkeitstheorie. Die Statistik beschäftigt sich mit dem Untersuchen und Auswerten großer Datenmengen. Die Wahrscheinlichkeitstheorie untersucht mit Hilfe von Experimenten die Gesetzmäßigkeiten zufälliger Ereignisse.
Die Formeln finden Sie im Buch ¹ auf den Seiten 50f (Wahrscheinlichkeitsrechnung) und auf Seite 8f (Mengen).
Zufallsversuch:
Ein Zufallsversuch ist ein Experiment, welches unter gleichen Bedingungen durchgeführt wird und einen nicht vorhersehbaren Ausgang hat. Der Ausgang des Experiments heißt Ergebnis.
Ergebnismenge:
Die Menge aller möglichen Ergebnisse eines Zufallsexperiments bezeichnet man als den Ergebnisraum Ω.
Beispiel:
Ein idealer Würfel wird geworfen. Ideal bedeutet, dass jedes Element der Ergebnismenge Ω (1,2,3,4,5,6) mit gleicher Wahrscheinlichkeit eintritt.
Ereignisse:
Ein Ereignis wird vor der Durchführung eines Zufallsexperiments angegeben. Es ist der "Wunsch", ein bestimmtes Ergebnis zu erhalten. Ereignisse werden mit Großbuchstaben beschriftet und sind eine Teilmenge des Ergebnisraumes Ω. Die Menge aller Teilmengen ist der Ereignisraum.
Beispiel:
Ereignis E1: "Es wird eine 3 gewürfelt."
Ereignis E2: "Es wird eine gerade Zahl gewürfelt."
Ereignis E3: "Die geworfene Zahl ist durch 3 teilbar."
Ereignis E4: "Es wird eine gerade oder eine ungerade Zahl gewürfelt."
Ereignis E5: "Es wird eine 8 gewürfelt."
Das Ereignis E1 ist ein Elementarereignis.
Es enthält ein einziges Element aus dem Ergebnisraum Ω.
Das Ereignis E4 ist ein sicheres Ereignis.
Es enthält alle Elemente aus dem Ergebnisraum Ω und wird daher eintreten.
Das Ereignis E5 ist das unmögliche Ereignis, da keine 8 gewürfelt werden kann.
Mengenoperationen:
Aus zwei Ereignissen kann durch Mengenoperationen ein neues Ereignis gebildet werden.
Durchschnitt, Schnittmenge
Sind A und B zwei Ereignisse, so tritt A ∩ B genau dann ein, wenn sowohl das Ereignis A als auch
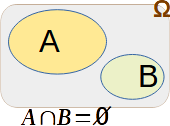
das Ereignis B eingetreten ist. Entsteht dabei eine leere Menge, so nennt man die Ereignisse A und B
unvereinbar.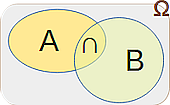
Vereinigung
Sind A und B zwei Ereignisse, so tritt A ∪ B genau dann ein, wenn mindestens eines der Ereignisse
eingetreten ist.
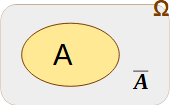
Komplement
Ein Komplement ist das Gegenereignis. (Hinweis: Als Zeichen kann der Überstrich oder ¬ verwendet werden.)
Es gibt weitere Verknüpfungsmöglichkeiten. Diese werden hier jedoch nicht weiter betrachtet.
Häufigkeit:
Man führt ein Zufallsexperiment mehrfach durch und notiert für ein gegebenes Ereignis E die
Häufigkeit seines Eintretens. Damit erhält man die absolute Häufigkeit H(E)
des Eintretens des Ereignisses.
Setzt man die absolute Häufigkeit in das Verhältnis zur Gesamtanzahl n
der durchgeführten Versuche, dann erhält man die relative Häufigkeit h(E).
Beispiel:
Wurde das Würfeln 50x ausgeführt und das Ereignis E1 ist dabei 12x eingetreten, so sind H(E1) = 12 und h(E1) = 12/50 = 0,24 bzw. 24%.
Wahrscheinlichkeit P
Für die mathematische Wahrscheinlichkeit P des Eintretens eines Ereignisses E gilt: 0 ≤ P(E) ≤ 1
Sie lässt sich auf drei Arten bestimmen:
- Bei einer großen Anzahl von Wiederholungen eines Zufallsexperimentes kann die relative Häufigkeit als Wahrscheinlichkeit P des Eintretens eines Ereignisses angesehen werden. Es gilt: P(E)=h(E)
- Die klassische Definition der Wahrscheinlichkeit geht davon aus, dass jedes mögliche Elementarereignis
eines Zufallsversuchs mit gleicher Wahrscheinlichkeit eintritt. Solche Versuche nennt man auch Laplace-Experiment.
P(E) = 1/n (n: Anzahl der Elementarereignisse) - Eine Verallgemeinerung beschrieb A. N. Kolmogorow mit dem Axiomensystem der Wahrscheinlichkeitstheorie und den zugehörigen Rechenregeln.
Kombinatorik
Kombinatorik ist die Lehre vom Abzählen. Gezählt werden Kombinationsmöglichkeiten, Auswahlen oder die Elemente von Mengen.
Man bestimmt die Anzahl mittels ...
- einer Liste,
- einem Baumdiagramm oder
- der Permutationsregel.
Beispiel:
 Wie viele Möglichkeiten der Anordnung gibt es?
Wie viele Möglichkeiten der Anordnung gibt es?

Liste: 6 Möglichkeiten
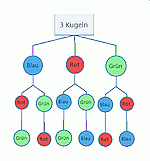
Baumdiagramm: 6 Endknoten, d. h.
6 Möglichkeiten
Permutationsregel:
6! = 6 · 5 · 4 · 3 · 2 · 1 = 720