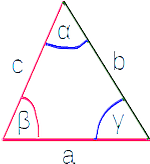
Dreieck:
Ein Dreieck besitzt drei Seiten, drei Ecken und drei Winkel. Die mathematische Bezeichnung ist ΔABC.
Die Summe der Innenwinkel beträgt 180°.
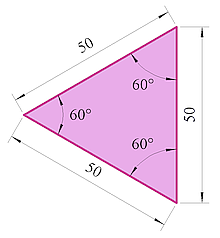
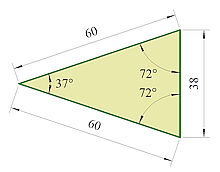
Für das rechtwinklige Dreieck existiert eine eigene Webseite. Bei ungleichseitigen Dreiecken liegt der größte Innenwinkel der längsten Seite gegenüber.
Viereck:
Vierecke haben vier Seiten, vier Ecken und vier Winkel. Die Summe der Innenwinkel ist 360°.
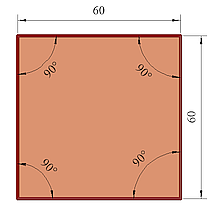
Die Innenwinkel betragen jeweils 90°.
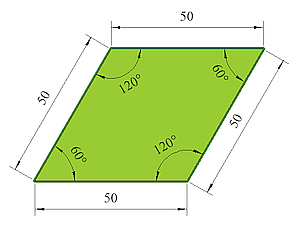
Gegenüberliegende Winkel sind gleich groß.
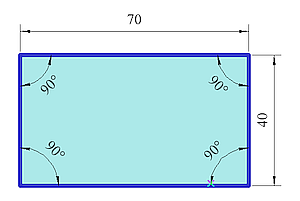
Die Innenwinkel betragen jeweils 90°.
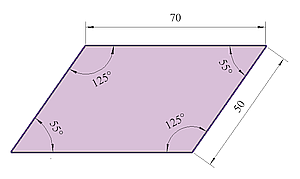
Gegenüberliegende Winkel sind gleich groß.
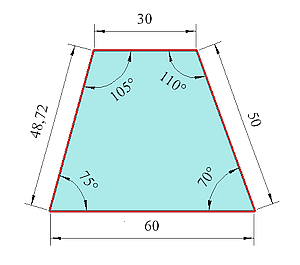
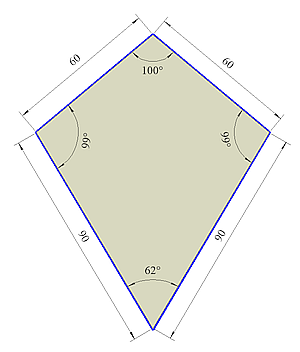
Es gibt ein Paar gleich große Winkel.
Polygon:
Ein Polygon hat mindestens drei Seiten und drei Winkel. Somit ist das Dreieck das "kleinste" Polygon.
Bei einem regelmäßen Polygon (n-Eck) sind alle Seiten gleich lang und alle Winkel gleich groß. Bei einem unregelmäßen Polygon ist mindestens eine Seitenlänge unterschiedlich.
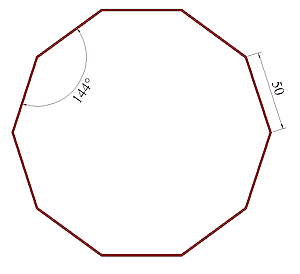
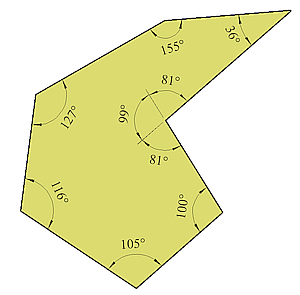
Die Summe der Außenwinkel eines Polygons beträgt 360°. Die Summe der Innenwinkel ist von der Anzahl der Seiten abhängig und kann größer als 360° sein.
Symmetrie:
Es gibt bei Polygonen zwei Arten von Symmetrien: Achsensymmetrie (Spiegelung) und Drehsymmetrie.
Drehsymmetrie bedeutet, dass bei Drehung um einen bestimmten Punkt die Figur deckungsgleich auf sich selbst abgebildet werden kann.
Bei Achsensymmetrie kann eine Figur durch Spiegelung an einer Symmetrieachse auf sich selbst abgebildet werden.
Beispiele:- Die Figur "Drachen" ist achsensymmetrisch.
- Ein gleichseitiges Dreieck ist achsensymmetrisch und auch drehsymmetrisch.
Sinussatz:
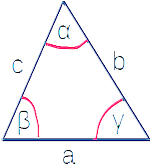
Der Sinussatz gilt in allen Dreiecken. Es gilt: a/(sin α) = b/ (sin β) = c/(sin γ)
Kosinussatz:
Der Kosinussatz gilt in allen Dreiecken. Es gilt für die Seite b:
b² = a² + c² − (2·a·c·cos β)
Diese Formel kann analog dazu für jede Seite aufgestellt werden.