Begriff und Anwendung
Lineare Optimierung beschäftigt sich mit der Optimierung einer linearen Zielfunktion z, welche durch Nebenbedingungen eingeschränkt ist. Es handelt sich dabei um ein System aus linearen Gleichungen und Ungleichungen.
Sie ist eines der Hauptverfahren des Operations Research Dies ist Teilgebiet der Angewandten Mathematik. (bzw. Operational Research).
Anwendungsgebiete sind z. B.
- die Produktionsplanung
- das Mischen verschiedener Stoffe
- Investitionsplanungsprobleme
- Transport und Logistik
- Zuordnungsprobleme
- Verschnittprobleme
Grafisches Lösen
Beispiel:
Gegeben sind die folgenden Nebenbedingungen:
(1) 0 ≤ x ≤ 3
(2) y ≥ 0
(3) y −3 · x + 1 ≥ 0
(4) 2 · y ≤ 5 − 4 · x
Es gilt: x ∈ R.
Die Zielfunktion z lautet: z = 2 · x + 3 · y → Maximieren
Beim grafischen Lösen werden die Nebenbedingungen im Koordinatensystem eingetragen und die gemeinsame Punktmenge bestimmt. Diese wird auch Planungsvieleck genannt. Die Eckpunkte können das gesuchte Ziel sein.
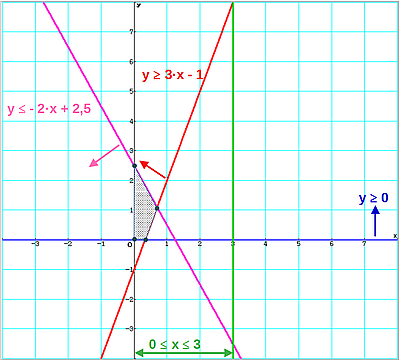
Beim Auffinden des Planungsvielecks kann es hilfreich sein, die relevante Lösungsmenge einer
Nebenbedingung durch Pfeile zu kennzeichnen. Die Gerade selbst erfüllt die Gleichung
y = m · x + n. Um die richtige Punktmenge der Ungleichung
y > m · x + n oder y < m · x + n
zu finden, setzt man einen beliebigen Wert für x ein und berechnet y.
Beispielsweise gilt für
x = 0 in Gleichung (3): y + 1 ≥ 0. Damit erfüllen alle y
größer als -1 die Ungleichung.
Wenn man den GTR verwendet, so schraffiert dieser die Lösungsmenge, wenn man einen anderen Typ als "=" einstellt.
Nun werden für alle gewonnenen Eckpunkte des Planungsvielecks die Werte für z berechnet. Hierfür müssen zunächst die Koordinaten der Punkte berechnet werden.
- P1(0;0): z = 2 · 0 + 3 · 0 = 0
- P2(1/3;0): z = 2 · 1/3 + 3 · 0 = 2/3 (P2: Nullstelle der Funktion y = 3 · x - 1.)
- P3(0,7;1,1): z = 2 · 0,7 + 3 · 1,1 = 4,7 (P3: Schnittpunkt der Funktionen y = 3 · x - 1 und y = −2 · x + 2,5.)
- P4(0;2,5): z = 2 · 0 + 3 · 2,5 = 7,5
Die Funktion z besitzt ihr Maximum bei x = 0 und y = 2,5.
Simplex-Algorithmus
Die grafische Lösung ist bei geeigneten Zahlenwerten und zwei Variablen einsetzbar. Ab drei Variablen ist eine rechnerische Suche nach der Lösung sinnvoll.
Die (Un)Gleichungen anpassen
Um das Simplex-Verfahren verwenden zu können, muss für alle Variablen gelten, dass ihre Werte positiv sind (≥0). Alle Ungleichungen müssen so umgestellt werden, dass sich alle Variablen auf der linken Seite befinden und ein ≤-Zeichen besitzen. Alle Absolutglieder befinden sich auf der rechten Seite.
Für das Beispiel ergeben sich folgende Ungleichungen:
(1) x ≤ 3
(2) 3 · x − y ≤ 1 (Die Ungleichung wurde mit −1 multipliziert , um ein ≤ zu erhalten.)
(3) 4 · x + 2 · y ≤ 5
(4) − 2 · x − 3 · y + z = 0
Aus den bisherigen Ungleichungen (1) und (2) ergeben sich außerdem x ≥ 0 und y ≥ 0. Diese Nebenbedingungen sind die Voraussetzung für die Anwendung des Simplex-Verfahrens und werden in der folgenden Berechnung nicht mehr aufgeführt.
Schlupfvariablen einfügen
Durch sogenannte "Schlupfvariablen" werden die Ungleichheitszeichen beseitigt.
Für das Beispiel ergibt sich:
(1) x + s1 = 3
(2) 3 · x − y + s2 = 1 (Die Ungleichung wurde mit −1 multipliziert , um ein ≤ zu erhalten.)
(3) 4 · x + 2 · y + s3 = 5
(4) − 2 · x − 3 · y + z = 0
Die Tabelle aufstellen
| x | y | s1 | s2 | s3 | z | b | |
|---|---|---|---|---|---|---|---|
| s1 | 1 | 0 | 1 | 0 | 0 | 0 | 3 |
| s2 | 3 | −1 | 0 | 1 | 0 | 0 | 1 |
| s3 | 4 | 2 | 0 | 0 | 1 | 0 | 5 |
| z | −2 | −3 | 0 | 0 | 0 | 0 | 0 |
Die Basislösung bestimmen
Man setzt x = 0 und y = 0 in die Gleichungen ein und berechnet die Schlupfvariablen
sowie den Wert für z:
s1 = 3
s2 = 1
s3 = 5
z = 0
Eine Spalte mit einer Zeile tauschen
Für den Tausch wählt man die Variablenspalte aus, die in der Zielfunktion die größte gewünschte Änderung bewirkt.
Im Beispiel ist z zu maximieren. Die Variable y bringt mit dem Faktor 3 den größeren Wertzuwachs.
Man berechnet nun in jeder Zeile den Quotienten b/y. Die Zeile mit dem kleinsten positiven Wert wird zum Tausch ausgewählt. Das Element an der Kreuzung von Zeile und Spalte nennt man Pivotelement (PE).
| x | y | s1 | s2 | s3 | z | b | b/y | |
|---|---|---|---|---|---|---|---|---|
| s1 | 1 | 0 | 1 | 0 | 0 | 0 | 3 | n. l. |
| s2 | 3 | −1 | 0 | 1 | 0 | 0 | 1 | −1 |
| s3 | 4 | 2 | 0 | 0 | 1 | 0 | 5 | 2,5 |
| z | −2 | −3 | 0 | 0 | 0 | 0 | 0 | 0 |
Die Zeilen müssen nun so umgeformt werden, dass in der Spalte y die Werte der Spalte s3 entstehen.
Zuerst dividiert man jedes Element der Pivotzeile durch das Pivotelement. Anschließend addiert bzw. subtrahiert man ein Vielfaches der Pivotzeile zu den restlichen Zeilen.
| x | s3 | s1 | s2 | s3 | z | b | |
|---|---|---|---|---|---|---|---|
| s1 | 1 | 0 | 1 | 0 | 0 | 0 | 3 |
| s2 | 5 | 0 | 0 | 1 | 0,5 | 0 | 3,5 |
| y | 2 | 1 | 0 | 0 | 0,5 | 0 | 2,5 |
| z | 4 | 0 | 0 | 0 | 1,5 | 0 | 7,5 |
In der Zeile s2 muss die Pivotzeile addiert werden. In der Zeile z wird das Dreifache der Pivotzeile addiert.
Aus der Tabelle ergibt sich in der Spalte b eine weitere Lösung: x = 0, y = 2,5 und z = 7,5.
Dieser Schritt wird solange wiederholt, bis sich in der Zeile z keine negativen Zahlen mehr befinden. Da dies im Beispiel der Fall ist, wurde das gesuchte Maximum gefunden.