Inhalt:

Eigenschaften von Funktionen und Begriffe

Ordnen Sie den Abbildungen den Begriff Relation bzw. Funktion zu. Begründen Sie Ihre Aussage.

Beispiel 1

Beispiel 2

Beispiel 3

Beispiel 4

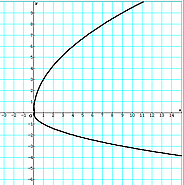
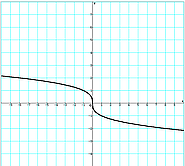
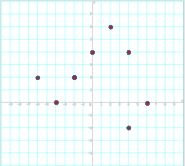
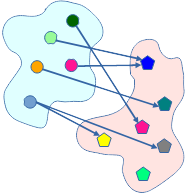
Quadratische Funktionen

Ermitteln Sie aus den gegebenen Angaben die Funktionsgleichung f(x) der quadratischen Funktion in der Form a · x² + b · x + c.

1. Scheitelpunkt S(4;−1); Nullstelle N₁(2;0)

Lineare Funktion

Ein Fahrzeug hat einen maximalen Tankinhalt von 45 Litern. Auf 100 km verbraucht es 4,2 Liter.

1. Geben Sie eine Funktion f(x) an, mit der in Abhängigkeit der gefahrenen Kilometer der Tankinhalt bestimmt werden kann.
2. Nach wie vielen Kilometern ist der Tank leer?

Polynomfunktion

Gegeben ist die Funktion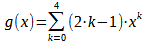

Ermitteln Sie die einzelnen Summanden und notieren Sie die Funktionsgleichung von g(x).

Exponentialfunktion/Logarithmus

a) Wachstumsvorgänge können mit der Funktionsgleichung f(x) = a · e ^k · x beschrieben werden. Bei einem prozentualen Wachstum gilt k = p/100.

Ein Grashalm ist 2 cm lang. Welche Länge hat er nach einem Monat (30 Tage), wenn er 4% pro Tag wächst. Nach wie vielen Tagen ist der Grashalm 5 cm lang?

b) Bestimmen Sie die Definitions- und Lösungsmenge der folgenden Gleichungen:

• log₂(2 · x + 6) = 4 + log₂ (x − 2)
• log₄(x³) = 3 + log₄(2)

Periodische Funktionen

a) Ermitteln Sie die Lösungen der nachfolgenden Gleichungen.

1. sin φ = -0,4067 für φ ∈[0°;360°]
2. cos φ = 0,1564 für φ ∈[0°;360°]
3. tan φ = 1,1542 für φ ∈]180°;270°[

b) Ein stumpfer Winkel ist durch tan φ = − 0,5 gegeben. Berechnen Sie den Wert von sin φ und cos φ.

c) Berechnen Sie den Neigungswinkel zweier Seitenflächen eines regulären Tetraeders.

Umkehrfunktion

a) Gegeben ist die Funktionsgleichung f(x) = (2 · x + 1)^0,5.

Geben Sie den Definitionsbereich und den Wertebereich der Funktion an. Begründen Sie mit Hilfe des Schaubildes, dass die Funktion umkehrbar ist. Ermitteln Sie alle Angaben zur Umkehrfunktion.

b) f(x) = x² + 3·x

Geben Sie den den Definitionsbereich und den Wertebereich der Funktion an. Begründen Sie mit Hilfe des Schaubildes, dass die Funktion nicht umkehrbar ist. Geben Sie einen Definitionsbereich an, in welchem eine Umkehrfunktion möglich wäre.

Zugelassene Hilfsmittel

Formelsammlung, Taschenrechner