Erläuterungen und Beispiele finden Sie im Buch ² ab Seite 9. Eine zusammenfassende Darstellung befindet sich im Buch ¹ auf der Seite 9.
Die nachfolgende Bezeichnung der Zahlenmengen orientiert sich an den Vorgaben der DIN.
Natürliche Zahlen:
Die Menge der natürlichen Zahlen wird zum Zählen verwendet. Über die Zugehörigkeit der Null wird immer wieder diskutiert. Wir verwenden N = {0, 1, 2, 3, 4, 5, ...}. Mit N* schließt man die Null aus: N* = {1, 2, 3, 4, 5, ...} = N\{0}
Die Grundrechenarten Addition und Multiplikation sind uneingeschränkt ausführbar.
Zahlen, die bei der Division durch 2 den Rest 0 ergeben, werden gerade Zahlen genannt. Die Null ist eine gerade Zahl.
Ganze Zahlen:
Die Menge der ganzen Zahlen Z entsteht, wenn man die natürlichen Zahlen mit negativen Zahlen ergänzt.
Dabei gilt: n ∈ N, n + (-n) = 0
Z = {..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...} oder Z = {0, 1, -1, 2, -2, 3, -3, 4, -4, 5, -5, ...}.
Mit Z* schließt man die Null aus: Z* = {..., -5, -4, -3, -2, -1, 1, 2, 3, 4, 5, ...} = Z\{0}
Die Grundrechenarten Addition, Subtraktion und Multiplikation sind uneingeschränkt ausführbar.
Rationale Zahlen:
Die Menge der rationalen Zahlen enthält alle Zahlen, die sich als Bruch darstellen lassen. Dabei ist der Zähler des Bruches eine ganze Zahl und der Nenner eine Zahl aus der Menge N*. Mit Q* schließt man die Null aus.
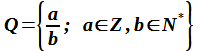
Führt man die Division aus, so entsteht die Dezimaldarstellung des Bruches. Rationale Zahlen sind in der Dezimaldarstellung entweder endlich oder periodisch.
Beispiele:
1/8 = 0,125 (endlich); 13/7 = 1,857142857142... (periodisch)
Die Grundrechenart Division und weitere höhere Rechenoperationen (z. B. das Wurzelziehen) sind nicht uneingeschränkt ausführbar.
Reelle Zahlen:
Die Menge der rationalen und der irrationalen Zahlen ergibt die Menge der rellen Zahlen R. Mit R* schließt man die Null aus.
Irrationale Zahlen:
Eine Zahl, deren Dezimaldarstellung unendlich und nicht periodisch ist, gehört zur Menge der irrationalen Zahlen.
Beispiel: √3 = 1,7320508... (unendlich, nicht periodisch); Kreiszahl π; Eulersche Zahl e
Die Grundrechenarten (außer die Division durch 0) und weitere höhere Rechenoperationen sind uneingeschränkt ausführbar. Das Wurzelziehen ist weiterhin eingeschränkt. √-2 ist im Bereich der reellen Zahlen nicht lösbar.
Zahlenstrahl und Intervalle:
Auf einer Geraden wird ein Punkt der Zahl Null zugeordnet (Ursprung). Rechts von der Zahl Null wird ein weiterer Punkt der Zahl 1 zugeordnet. Damit entsteht eine Strecke, welche dem Einheitsintervall [0;1] (Einheitsstrecke) entspricht. Negative Zahlen liegen links vom Ursprung.
Alle rationalen Zahlen werden als das a/b-Vielfache der Einheitsstrecke dargestellt. Irrationale Zahlen werden durch eine Intervallschachtelung bestimmt.
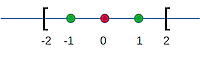
Gehören die Zahlen an den Intervallgrenzen zur dargestellten Menge, so nennt man dies ein geschlossenes Intervall. D. h. es gibt eine kleinste und eine größte Zahl im Intervall.
Beispiel: