Begriff Menge:

Der Begründer der Mengenlehre, Georg Cantor (1845-1918), beschrieb den Begriff Menge mit folgender Aussage:
"Eine Menge ist eine Zusammenfassung von bestimmten wohl unterschiedenen Objekten unserer Anschauung oder unseres Denkens, welche die Elemente der Menge genannt werden, zu einem Ganzen."

In der Mathematik gelten folgende Festlegungen:

• Eine Menge ist nur dann festgelegt, wenn sich von den Objekten angeben lässt, ob sie zur Menge gehören oder nicht.
• Ein Objekt kann nicht mehrfach Element der Menge sein.
• Mengen werden mit Großbuchstaben bezeichnet. Die Elemente werden mit Kleinbuchstaben bezeichnet.

• Die Menge, die kein Element aus dem Grundbereich G enthält, heißt leere Menge: ∅
• Die Menge, die alle Elemente des Grundbereichs G enthält heißt Allmenge.
• Mengen können nach der Anzahl ihrer Elemente benannt werden.

Darstellung:

Aufzählung

Die Elemente der Menge werden in geschweifte Klammern gesetzt und durch Komma getrennt. Um bei Dezimalzahlen Verwechslungen mit dem Dezimalkomma zu vermeiden, kann auch ein Semikolon verwendet werden.
Beispiele:   A = {a, b, c}     B = {1, 2, 3, 5}

Beschreibung

Innerhalb der geschweiften Klammern wird eine Regel formuliert, mit deren Hilfe sich die Elemente der Menge bilden lassen bzw entschieden werden kann, ob ein Objekt zur Menge gehört oder nicht.
Beispield: C = {x | x ist eine Primzahl.}    D = {n | n ist eine gerade natürliche Zahl und größer als 0.}

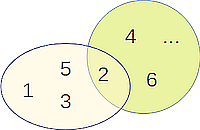
Venn-Diagramm

Mit einem Venn-Diagramm lassen sich alle Beziehungen (Relationen) zwischen den betrachteten Mengen darstellen.

Mengenoperationen:

Mengen lassen sich miteinander verknüpfen.

Beispiele:

• Vereinigungsmenge: A ∪ B = {a, b, c, 1, 2, 3, 5}
  Alle Elemente, die zu A oder zu B gehören.
• Schnittmenge: A ∩ B = {} = ∅
  Alle Elemente, die sowohl zu A als auch zu B gehören.
• Differenzmenge B \ D = {1, 3, 5}
  Alle Elemente, die zu B und nicht zu D gehören.
• Paarmenge A Χ B = {(a;1), (a;2), (a;3), (a;4), (a;5), (b;1), ..., (c;4), (c;5)}
  Alle geordneten Paare, dessen erstes Element zu A gehört und dessen zweites Element zu B gehört.